A simple glitch filter

This very simple filter is used to suppress stochastic (random) measurement errors. It is characterized by low CPU requirements (memory usage and computing time). The disadvantage is a delay of the measurement signal and a complex filter equation. For an exact mathematical calculability, it is certainly better to use other digital filters.

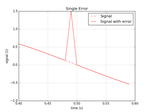
When measuring physical signals, stochastic errors can occur which massively influence a control circuit or can falsely distort an average value. The cause of these measurement errors are extensive, but "line faults" (eg short-circuit to earth of a signal line) and "bit errors" occur most frequently. In common with these errors is a strong short signal change occurs.

The above picture shows a disturbance: a very steep rise to a high measured value. A classic PID controller will surely react to this.

A remedy is to make a following control loop "stable" against such errors - but this would slow the controller reaction significantly.

As a further simple remedy, the signal can be treated with the help of a "moving average" - the error is "reduced" by means of the mean. The filtered signal will be delayed to the original signal, thus increasing the group run time of the control path. This must be taken into account when designing the control loop.

But even with this measure, there is still a markedly high value with a steep rise.

An improvement can be achieved if the values ​​which are used for the averaging are checked before the mean value calculation for minima and maxima. The values will not used for the calculation of the mean value.

The following figure illustrates this: The "Smart Average" curve shows the curve of the selected method.

The influence of the disturbance is visibly minimized without a further deterioration of the group running time. Also typical "double errors" caused by the "swing back" of the signal will be filtered out.

The physical system is important for the interpretation of the discussed filter. Can only positive "outliers" occur? How long is a typical disorder? This information define how much "maximum/minimum" values ​​are filtered out and whether only "positive", "negative" or both values ​​have to be filtered.

Example

The following sample code shows a possible implementation of this filter.

/************************************************************************/
/* helper functions                                                     */
/************************************************************************/
void data_filter_find_int_min_max(int16_t *data_array, uint16_t array_size, uint16_t *min_position, uint16_t *max_position)
{
    int16_t min_val, max_val;
    uint16_t    i;
    uint16_t    min_pos, max_pos;

    min_val = INT16_MAX;
    max_val = INT16_MIN;
    min_pos = 0;
    max_pos = array_size -1;

    /* first run to determine the max/min values */
    for (i=0; i<array_size; i++) {
        if (data_array[i]>max_val) {
            max_val = data_array[i];
            max_pos = i;
            } else if (data_array[i]<min_val) {
            min_val = data_array[i];
            min_pos = i;
        }
    }

    *min_position = min_pos;
    *max_position = max_pos;
}

/************************************************************************/
/* Simple Min-Max removing averaging filter                             */
/************************************************************************/
int16_t data_filter_mima_array_int(int16_t *data_array, uint16_t array_size)
{
    int32_t sum;
    uint16_t    i, min_pos, max_pos;

    sum = 0;

    data_filter_find_int_min_max(data_array, array_size, &min_pos, &max_pos);

    for (i=0; i<array_size; i++) {
        if ((i!=max_pos) && (i!=min_pos))
        {
            sum += (int32_t)(data_array[i]);
        }
    }
    sum /= (array_size-2);

    return (int16_t) sum;
}

If you have any questions, suggestions or feedback, please do not hesitate to contact us via e-mail.